
A fűtési rendszerek megfelelő beszabályozása elengedhetetlen ahhoz, hogy az egyes helységek tervezett hőmérsékletét biztosítani lehessen. Manapság a precíz beszabályozás már nem okoz különösebb problémát, azonban néhány évtizeddel ezelőtt ez még közel sem volt elmondható. A XX. század második felének épületgépészei számos módszert kidolgoztak a probléma megoldására, ám Magyarországon egészen az 1980-as évek legelejéig egyetlen megoldás sem született, amivel a tervező által előírt tömegáramokat minden körülmények között biztosítani lehetett volna. Az áttörést Csohány Kálmán 1978-ban elkészült diplomamunkája hozta el, amiben a szerző külföldi mérnökök munkáját felhasználva dolgozta ki a megfelelő pontossággal működő beszabályozást.
Házgyári lakóépületek helyiséghőmérsékleti anomáliája
Csohány dolgozatának alapjául a házgyári lakóépületekben jelentkező helységhőmérsékleti anomália szolgált. A házgyári lakóépületekben a fűtési rendszer általában felső elosztású, egycsöves rendszer volt, ahol az épületben a párhuzamosan futó összekötő vezetékek1 szállították a fűtőközeget. A hőmérsékleti anomália azt jelentette, hogy az ily módon épített társasházak függőleges hőmérsékleteloszlásában jelentős eltérések voltak. A felső szinteken erőteljes túlfűtés mutatkozott, míg az alsó szinteken még maximális teljesítmény mellett sem sikerült a tervezett helységhőmérsékletet elérni2.
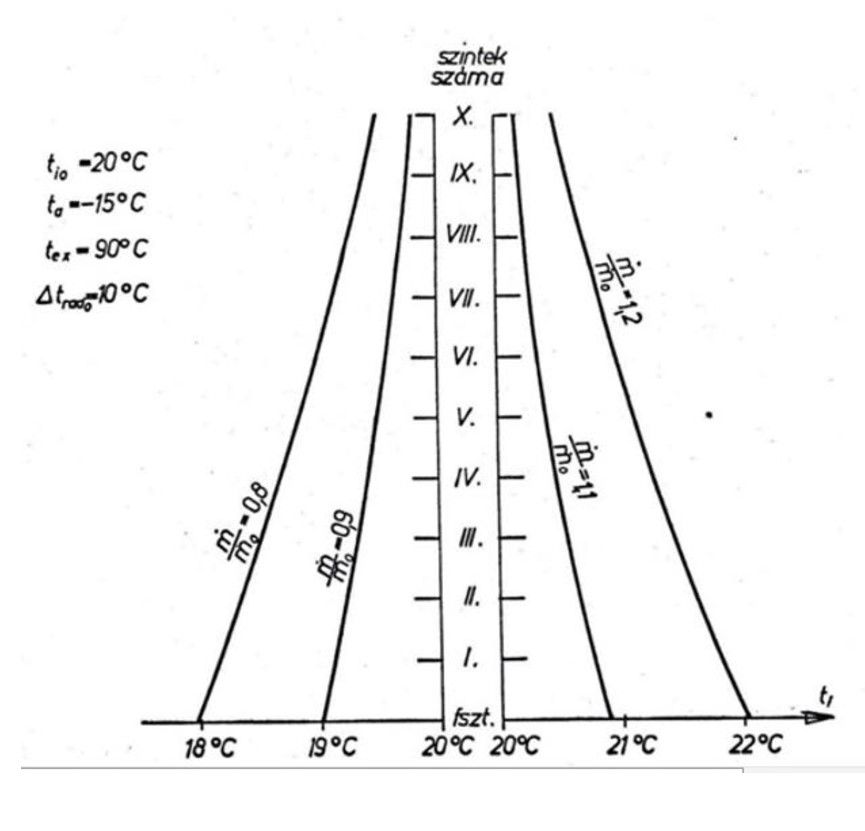
Az 1. ábra egy 10 emeletes épület egyik összekötő vezetéke mentén mutatja a tervezettől eltérő tömegáramok helyiséghőmérsékletre gyakorolt hatását. A számításokat -15°C-os külső hőmérséklet és 20°C-os helyiséghőmérséklet esetén végezték 90°C-os előremenő hőmérsékletet és 10°C-os hőmérsékletkülönbséget feltételezve a hőleadó előremenő és visszatérő vízhőmérséklete között.
A mérő-szabályozó egység
A kidolgozott módszer alkalmazhatóságának legfontosabb lépése az 1976-ra kifejlesztett mérő-szabályozó egység volt, ami képes volt egy adott csőszakasz tömegáramát méréssel meghatározni. Mindez nem csak azért számított jelentős áttörésnek mert ezelőtt Magyarországon egyetlen eszköz sem létezett, amivel egy épület fűtési rendszerének tömegáramát mérni lehetett volna, hanem azért is, mert a tömegáram mérhetősége nélkül a beszabályozáshoz a mérnökök csakis a hőmérsékletváltozásra tudtak hagyatkozni. Mivel a hőmérsékletváltozás hatásai csak órákkal a szelepállítást követően jelentkeznek, ez a módszer rendkívül körülményessé tette a beszabályozást. Az új eszköz nem volt más, mint egy csőszakasz két nyomáskivezetővel és egy szabályozó szeleppel (1. kép).

Maga a mérő-szabályozó egység nyomáskülönbséget mért, amiből a keresett tömegáramot egy erre a célra készített diagram segítségével lehetett megállapítani. A megfelelő pontosságú méréshez kellően nagy nyomáskülönbséget kellett létrehozni, amit az adott csőszakasz belső átmérőjének szűkítésével értek el. A kisebb csőátmérő meghatározására külön méretezés szolgált, melynek értéke többek között a csőben áramló tömegáramtól és a közeg sűrűségétől függött3.
A műszer kifejlesztése azért volt óriási lépés, mert így lehetőség nyílt egy adott szelep állítása során jelentkező hatások azonnali értékelésére. Maga a szerkezet azonban nem oldotta meg rögtön a beszabályozással járó összes problémát, ugyanis hiába lehetett tudni az adott összekötő vezetékben áramló fűtővíz tömegáramát, arról semmi információval nem szolgált, hogy egy szelep állítása hogyan befolyásolja a többi felszálló tömegáramát. Ez a probléma pedig az egész fűtési rendszer beszabályozásának legnagyobb rákfenéje, ha ugyanis a csővezetéki rendszer egy pontján megváltozik az ellenállás, az az egész rendszerre hatással van. Így a korábban jó tömegáramra beállított szakaszokon átfolyó víz mennyisége is változni fog.
Módszer kidolgozása a beszabályozáshoz
A beszabályozás nehézségeinek ismeretében logikus célkitűzés volt egy olyan módszer kidolgozása, ami során minden szabályozó szelepen csak egyszer kell állítani, és minden mérő-szabályozó egységen csak egyszer kell a tömegáramot megmérni. Egy több tucat összekötő vezetéket tartalmazó rendszernél még ez is hosszadalmas tud lenni, azonban egy hálózat pontos működéséhez szükséges minden szelephez legalább egyszer hozzányúlni. Ezt egyáltalán nem könnyű megvalósítani, ugyanis egy párhuzamos körökből álló rendszer esetében bármilyen változtatás a rendszer minden pontján érezteti hatását. Hogy a célkitűzés megvalósítható legyen, olyan módszert kellett kidolgozni, ami előre megmondja, hogy egy adott felszállón milyen tömegáramot szükséges beállítani ahhoz, hogy az utolsó szabályozó szelep beállítása után minden összekötő vezetékre a tervezett tömegáram jusson. Ehhez a tervezési állapot mellett ismerni kell a kiinduló állapotot is, valamint azt is, hogy az egyes szelepek meghatározott értékre állításakor éppen milyen tömegáram-viszonyok vannak a rendszerben.
A kidolgozott módszer első lépésében a rendszerben található minden szabályozó szelep teljesen nyitva van. Ez mindenki számára kellő pontossággal definiálható alapállapot, amiben a szelepek nyitott állásához tartozó ellenállástényező és a szivattyú jelleggörbe ismeretében meghatározható, hogy a hálózat ilyen állapotában a szivattyú mennyi fűtővizet szállít. Ha szükséges, ekkor be lehet állítani a szivattyúhoz tartozó mérő-szabályozó egység segítségével a szállítandó tömegáramot, ugyanis ennek pontos beállítása nélkül a beszabályozást nincs értelme elkezdeni. A beszabályozás elvégzéséhez először meg kell határozni egy logikus sorrendet, ami mentén a szelepeket az előre meghatározott értékre állítják. Hogy a mérő-szabályozóval ne kelljen a névleges tömegáram töredékét mérni, érdemes a beszabályozást a szivattyúhoz közel kezdeni, mert kis tömegáramoknál a mérőműszer nagyobb hibával képes csak mérni. Az első szabályozó szelep végleges beállításakor még az összes többi szelep teljesen nyitott állapotban van. Ahhoz, hogy ezt a szelepet a megfelelő fojtásra állítsa a kivitelező, a tervezőnek a számítási módszer alapján meg kell adnia azt a tömegáramot, ami a szelepállítás után az adott felszállón megjelenik. Az első beszabályozó szelep beállítását követően a rendszer összes szelepét be kell állítani a tervező által meghatározott tömegáramra, és csakis az utolsó szelep beállítását követően fog a rendszer minden összekötő vezetékében a tervezési tömegáram áramlani. Leegyszerűsítve elmondható, hogy minden összekötő vezetéknél ismert egy ’ellenőrző tömegáram’ és egy ’beállítási tömegáram’. Előbbi az a tömegáram, ami az adott felszálló beállítása előtt áramlik a vezetékben, utóbbi pedig az a mennyiség, ami a szelep megfelelő fojtása után fog áramlani a csőben akkor, mikor a soron következő további szelepek még nyitott állapotban vannak. A számítási módszer szempontjából minden szelepállítás egy-egy üzemállapotnak felel meg. A számítást mindegyik üzemállapotra el kell végezni, és még ekkor is csak két összekötő vezetékre releváns a kapott tömegáram. Adott szelepállítás után az első összekötő vezetékben annak beállítási tömegárama az érdekes, valamint a következő felszálló tömegárama, ami annak ellenőrzési tömegárama lesz4, 5.
A matematikai modell kidolgozása
A házgyári lakóépületek fűtési hálózatát a matematikai modellben párhuzamos áramkörök segítségével modellezik. A modell felállításához szükség volt a csomóponti és hurokegyenletekre; valamint néhány további összefüggésre, illetve elhanyagolásra. Az egyszerűsítések szerint a rendszerbe épített elemek alaki és súrlódási ellenállástényezői a sebességtől függetlenek; a rendszerben turbulens áramlást feltételezünk; továbbá a sűrűséget is állandónak tekintjük, amivel a csővezetéki rendszer teljes szakaszán elhanyagoljuk a hőmérsékletváltozást.
A megfelelő beszabályozásra szolgáló modell megalkotásánál az épületgépészetben általánosan ismert egyenletből, a csőben áramló közeg nyomásveszteségéből indultak ki. A kontinuitási tétel segítségével a térfogatáram kifejezhető a sebességből, majd a kapott térfogatáramot a sűrűséggel megszorozva megkapjuk a rendszerben áramló víz tömegáramát. Az új egyenletet vizsgálva könnyen észrevehető, hogy a tömegáramot leszámítva minden paraméter állandónak tekinthető, amit ki lehet fejezni egyetlen tényezővel. A beszabályozási tényezőnek elnevezett ismeretlen segítségével, valamint két további törvény alkalmazásával az egyenlet olyan alakra hozható, ahol egy adott összekötővezeték tömegárama csakis a rendszer tömegáramától és a beszabályozási tényezőtől függ.
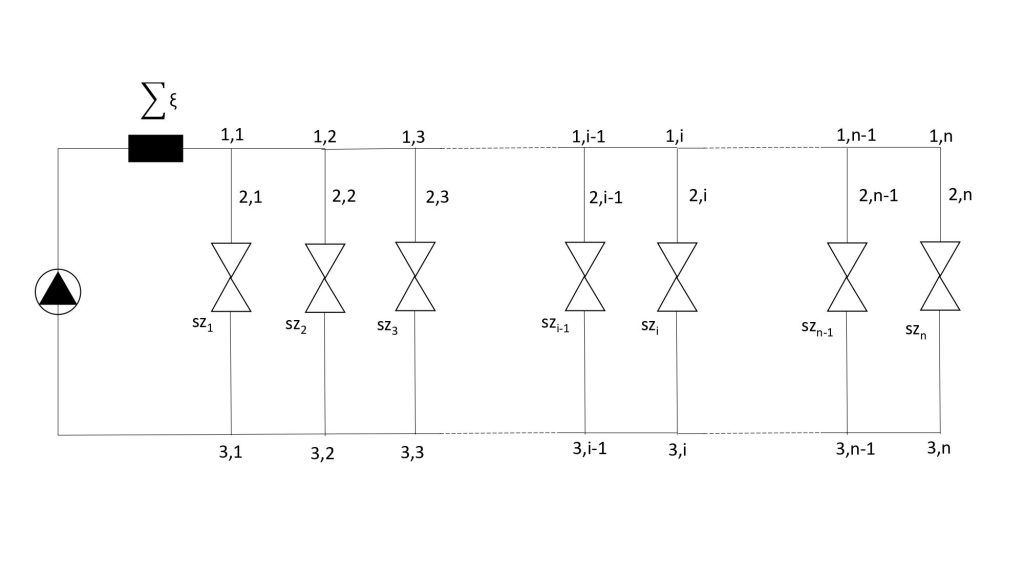
Valós épületgépészeti rendszerek esetén az összekötő vezeték két oldalán a nyomások nem egyeznek meg. A 2. ábrán látható modell nyomásviszonyaira igaz, hogy az 1,1 és 3,1 pontok közötti nyomáskülönbség megegyezik bármelyik olyan útvonal egyes szakaszain kialakuló nyomáskülönbségek összegével, amik az 1,1 pontból indulnak és a 3,1 pontban érnek véget (ezt írja le tulajdonképpen a hurokegyenlet). A korábban bevezetett beszabályozási tényezők segítségével felírható a bonyolult hurokegyenletet, amelynek közlésétől itt eltekintünk.
További megfontolások után a tömegáramok már egyszerű logika szerint meghatározhatóak – de mint azt az összefüggés is sejteti, az eljárás meglehetősen számításigényes.
Ahhoz, hogy a modell teljes mértékben megfeleljen a valóságnak, figyelembe kell venni a szivattyú munkapontváltozását is. Erre azért van szükség, mert ha a rendszer valamely pontján változik az ellenállás, az értelemszerűen együtt jár az egész rendszer eredő ellenállásának a megváltozásával, aminek hatására változik a szivattyú által szállított tömegáram is. Matematikai eszközökkel a munkapont könnyen számítható, ami után már csak megfelelő átalakításokat kell végezni az összefüggéseken, hogy a rendszerben keringtetett tömegáramot kifejező képletet megkapjuk. Ezzel a módszerrel a gyakorlatnak megfelelő pontosságú értéket kapunk az összekötő vezetékben áramló tömegáram nagyságára.
Az így kidolgozott modell képes volt arra, hogy bármely szelep tetszőleges állítása esetén kiszámítsa minden összekötő vezeték tömegáramát. Mivel az eredmények meghatározásához iterációra volt szükség, így már néhány összekötő vezetéket tartalmazó rendszerek esetén is olyan bonyolult és hosszadalmas volt a számítás, hogy feltétlenül szükség volt egy erre a célra írt számítógépes program használatára.
Bár az eredeti elképzelés az volt, hogy a tömegáramok számítására egy teljesen új programot készítenek, a modell bonyolultsága miatt végül egy akkor már évek óta használatban lévő modellt tettek be a számítógépes algoritmusba. Az Almásy-Budavári-Vajna féle számítási módszert nem beszabályozásra készítették, hanem a Fővárosi Vízművek használta arra a célra, hogy a budapesti ivóvíz közműhálózat tömegáramait számítsák. Ez a módszer néhány apró átdolgozás után ugyanazt tudta, mint a [3] szakdolgozatban kifejlesztett modell, csak sokkal rövidebb futásidővel.
A kidolgozott modell gyakorlati jelentősége
Az elmélet kidolgozása után a témában jártas mérnökök nekiláttak a modell pontosságát igazoló gyakorlati mérések kivitelezésének. Ennek során azt vizsgálták, hogy a program által szolgáltatott eredmények milyen viszonyban vannak egy laboratóriumi modellen mért értékekkel. Ehhez a Csőszer laborjában kiépítésre került egy 16 összekötő vezetékből álló kísérleti rendszer, ami egy valóságos rendszer minden elemét tartalmazta.
A vizsgálatok során arra a megállapításra jutottak, hogy amíg az alap – azaz a beszabályozás előtti – állapotban mért tömegáramok akár 15 %-kal is eltértek a számított tömegáramtól, addig a szelepek fojtását követően ez az eltérés mindössze már csak néhány százalék volt. Ennek oka, hogy a számítás során kapott tömegáramokat a szelep segítségével állították be a meghatározott értékre. Amíg nyitott szelepállások esetében a számítás a rendszerelemek akkoriban elfogadott ellenállástényezői alapján számította ki a tömegáramot, addig a beszabályozás során már a számított tömegáramot kellett a szelep segítségével beállítani, így a csővezeték kivitelezése során okozott hibákat a szelepállítással korrigálni lehetett. Emellett természetesen az épület valós állapota is eltérhet a tervezett állapottól, aminek kedvezőtlen hatásait a számítás szintén korrigálni tudja. Elmondható tehát, hogy a szelepek beállításával a rendszer hidraulikailag olyan állapotba hozható, ahogyan azt a tervező elképzelte.
Miután bebizonyosodott, hogy a modell a valóságnak megfelel, minden újépítésű lakóépület fűtési rendszerének beszabályozásához előírták az alkalmazását. Az ellenőrző mérések és a gyakorlat is bebizonyította, hogy a kidolgozott módszer kitűnően működött. Mire azonban használatát kötelezővé tették, kiderült, hogy a diplomamunka alapjául szolgáló jelenség legfőbb oka nem is a rossz beszabályozás, hanem a hőveszteségszámítás pontatlansága volt. Ettől függetlenül, az 1990-es évek elején Robert Petitjean és a T&A által kidolgozott, ma is használatban lévő modern beszabályozás elterjedéséig Magyarországon az előzőekben bemutatott módszer határozta meg a fűtési rendszerek kivitelezését. A hazai épületgépészet történetét tekintve összességében egy olyan jelentős szellemi teljesítményről és eredményről beszélhetünk, ami hosszú évtizedek után sikeresen oldotta meg a hazai épületgépészeti szakma egyik legnagyobb kihívását.

Tóth Krisztián
Jelenleg a BME első féléves MSc-s hallgatója, mellette egy épületgépész kivitelező cégnél dolgozik részmunkaidőben. 2020-ban szülővárosa egyik középiskolájában, az egri Neumann János Gimnázium és Kollégiumban érettségizett. 2024 januárjában a BME Gépészmérnöki Karán szerzett energetikai mérnök diplomát.
- mai szóhasználatban megfeleltethető a strangnak ↩︎
- Csőszeripari Vállalat Műszaki Fejlesztési Osztály: A fűtési rendszerek beszabályozási módszere (tanulmány) ↩︎
- Csőszeripari Vállalat Műszaki Fejlesztési Osztály: A fűtési rendszerek beszabályozási módszere (tanulmány) ↩︎
- Talpag József: Házgyári lakóépületek fűtési rendszereinek hidraulikai beszabályozási módszere (Épületgépészet 1980/3.)
↩︎ - Csohány Kálmán: Párhuzamos folyadékáramkörök beszabályozása (Diplomaterv, BME













